Study 7Z77 Main | 
Against All Odds
|
 by Richard Pavlicek by Richard Pavlicek |
What are the odds against being dealt a Yarborough? Or a singleton? Or 4-3-3-3 shape? Or an eight-card suit? Or all four aces? Or about anything else of interest or not. Check out the following tables for answers.
Each table lists a variety of hand types, the method of calculation*, the number of possible bridge hands, the percent probability (rounded to four decimal places) and the approximate odds against being dealt such a hand. In the few cases in which the odds favor a holding it is indicated simply as “favored.” For cases related to HCP, see the separate work on High Card Expectancy.
 *Combinatorial notation (NcR) is frequently used. Think of this as “N choose R” which means, given N items, the number of ways to select R of them. For example, 26c2 means “26 choose 2” which can be done in 325 ways; I could have just use the number 325, but the notation is more meaningful to show how the number is derived.
*Combinatorial notation (NcR) is frequently used. Think of this as “N choose R” which means, given N items, the number of ways to select R of them. For example, 26c2 means “26 choose 2” which can be done in 325 ways; I could have just use the number 325, but the notation is more meaningful to show how the number is derived.
 General Criteria
General Criteria
This table lists hand types based on general characteristics. Clarification of terms: A “Yarborough” has no card above a nine. “Flat” means 4-3-3-3 shape; “balanced” means 4-3-3-3, 4-4-3-2 or 5-3-3-2; “semibalanced” means 5-4-2-2 or 6-3-2-2; and “quasibalanced” means 4-4-4-1 or 5-4-3-1. (OK, I invented the last one.)
A “guaranteed 7 NT” hand must have all four aces and no possible loser regardless of the remaining distribution and opening lead; in other words, you can claim 13 tricks before the lead. Example:  A-K
A-K  A-K-Q-J-10-9-2
A-K-Q-J-10-9-2  A-K-Q
A-K-Q 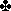 A, but note that changing the
A, but note that changing the  9 to the eight would disqualify it.
9 to the eight would disqualify it.
| Hand Type | Calculation | Hands | Percent | Odds Against
|
|---|
| Highest card 5 | 16c13 | 560 | 0.0000 | 1133952784:1
|
| Highest card 6 | 4c1·16c12+4c2·16c11+4c3·16c10+4c4·16c9 | 76,960 | 0.0000 | 8251215:1
|
| Highest card 7 | 4c1·20c12+4c2·20c11+4c3·20c10+4c4·20c9 | 2,418,624 | 0.0004 | 262551:1
|
| Highest card 8 | 4c1·24c12+4c2·24c11+4c3·24c10+4c4·24c9 | 34,946,016 | 0.0055 | 18171:1
|
| Highest card 9 | 4c1·28c12+4c2·28c11+4c3·28c10+4c4·28c9 | 309,931,440 | 0.0488 | 2048:1
|
| Highest card 10 | 4c1·32c12+4c2·32c11+4c3·32c10+4c4·32c9 | 1,963,416,000 | 0.3092 | 323:1
|
| Highest card J | 4c1·36c12+4c2·36c11+4c3·36c10+4c4·36c9 | 9,722,433,280 | 1.5311 | 65:1
|
| Highest card Q | 4c1·40c12+4c2·40c11+4c3·40c10+4c4·40c9 | 39,882,303,552 | 6.2805 | 15:1
|
| Highest card K | 4c1·44c12+4c2·44c11+4c3·44c10+4c4·44c9 | 141,012,722,864 | 22.2063 | 4:1
|
| Yarborough | 32c13 | 347,373,600 | 0.0547 | 1827:1
|
| Flat Yarborough | 4·8c33·8c4 | 49,172,480 | 0.0077 | 12913:1
|
| No card over 8 | 28c13 | 37,442,160 | 0.0059 | 16959:1
|
| Flat no card over 8 | 4·7c33·7c4 | 6,002,500 | 0.0009 | 105791:1
|
| Aceless | 48c13 | 192,928,249,296 | 30.3818 | 7:3
|
| One card each rank | (4c1)13 | 67,108,864 | 0.0106 | 9462:1
|
| Balanced | 4·13c3(13c4·13c32+3·13c42·13c2+3·13c5·13c3·13c2)=A | 302,292,822,832 | 47.6042 | 13:12
|
| Semibalanced | 12·13c22(13c5·13c4+13c6·13c3)=B | 103,012,900,848 | 16.2222 | 5:1
|
| Quasibalanced | 4·13c4·13c1(13c42+6·13c5·13c3)=C | 101,119,078,060 | 15.9239 | 5:1
|
| Balanced or semi- | A+B | 405,305,723,680 | 63.8263 | (favored)
|
| Semi- or quasi- | B+C | 204,131,978,908 | 32.1461 | 2:1
|
| Bal- semi- or quasi- | A+B+C | 506,424,801,740 | 79.7502 | (favored)
|
| All black cards | 26c13 | 10,400,600 | 0.0016 | 61054:1
|
| Guaranteed 7 NT | sum of all cases | 3756 | 0.0000 | 169066442:1
|
| 5 honors in any suit | 4·47c8-6·42c3 | 1,257,761,100 | 0.1981 | 504:1
|
| 4 honors in any suit | 5c4(4·47c9-6·5c4·42c5+4·5c42·37c1) | 27,125,401,200 | 4.2716 | 22:1
|
| 3 honors in any suit | 5c3(4·47c10-6·5c3·42c7+4·5c32·37c4-5c33·32c1) | 191,199,533,240 | 30.1095 | 7:3
|
| 2 honors in any suit | 5c2(4·47c11-6·5c2·42c9+4·5c22·37c7-5c23·32c5) | 468,318,386,680 | 73.7494 | (favored)
|
| 1 honor in any suit | 5c1(4·47c12-6·5c1·42c11+4·5c12·37c10-5c13·32c9) | 559,578,378,620 | 88.1207 | (favored)
|
| 2 tripletons | 6·13c32(26c7-2·13c3·13c4) | 122,114,884,320 | 19.2303 | 4:1
|
| 1 tripleton | 4·13c3(39c10-3·13c3(26c7-13c3·13c4)) | 282,345,395,904 | 44.4629 | 5:4
|
| At least 1 tripleton | 4·13c3·39c10-6·13c32·26c7+4·13c33·13c4 | 471,366,136,384 | 74.2293 | (favored)
|
| 2 doubletons | 6·13c22(26c9-2·13c2·13c7) | 104,286,598,416 | 16.4227 | 5:1
|
| 1 doubleton | 4·13c2(39c11-3·13c2(26c9-13c2·13c7)) | 304,584,314,112 | 47.9650 | 13:12
|
| At least 1 doubleton | 4·13c2·39c11-6·13c22·26c9+4·13c23·13c7 | 412,128,237,456 | 64.9007 | (favored)
|
| 2 singletons | 6·13c12(26c11-2·13c1·13c10) | 7,826,786,136 | 1.2325 | 80:1
|
| 1 singleton | 4·13c1(39c12-3·13c1(26c11-13c1·13c10)) | 187,700,354,296 | 29.5585 | 7:3
|
| At least 1 singleton | 4·13c1·39c12-6·13c12·26c11+4·13c13·13c10 | 195,529,653,800 | 30.7914 | 9:4
|
| 2 voids | 6(26c13-2) | 62,403,588 | 0.0098 | 10175:1
|
| 1 void | 4(39c13-3(26c13-13c13)) | 32,364,894,588 | 5.0967 | 19:1
|
| At least 1 void | 4·39c13-6·26c13+4·13c13 | 32,427,298,180 | 5.1066 | 19:1
|
| At least 1 sing./void | not 4333 4432 5332 5422 6322 7222 | 226,450,510,992 | 35.6607 | 9:5 |
| Study 7Z77 Main |  | Top Against All Odds |
 Hand Patterns
Hand Patterns
The following table lists the 39 generic hand patterns in their order of frequency. In each calculation the first number (4, 12 or 24) is the permutation factor for that pattern. For example, the generic pattern 4-4-3-2 can be permuted 12 different ways to form specific patterns. (See the second table for specific patterns.)
| Pattern | Freakness | Calculation | Hands | Percent | Odds Against
|
|---|
| 4-4-3-2 | 1 | 12·13c42·13c3·13c2 | 136,852,887,600 | 21.5512 | 7:2
|
| 5-3-3-2 | 2 | 12·13c5·13c32·13c2 | 98,534,079,072 | 15.5168 | 11:2
|
| 5-4-3-1 | 4 | 24·13c5·13c4·13c3·13c1 | 82,111,732,560 | 12.9307 | 13:2
|
| 5-4-2-2 | 3 | 12·13c5·13c4·13c22 | 67,182,326,640 | 10.5797 | 8:1
|
| 4-3-3-3 | 0 | 4·13c4·13c33 | 66,905,856,160 | 10.5361 | 17:2
|
| 6-3-2-2 | 4 | 12·13c6·13c3·13c22 | 35,830,574,208 | 5.6425 | 17:1
|
| 6-4-2-1 | 6 | 24·13c6·13c4·13c2·13c1 | 29,858,811,840 | 4.7021 | 20:1
|
| 6-3-3-1 | 5 | 12·13c6·13c32·13c1 | 21,896,462,016 | 3.4482 | 28:1
|
| 5-5-2-1 | 6 | 12·13c52·13c2·13c1 | 20,154,697,992 | 3.1739 | 31:1
|
| 4-4-4-1 | 3 | 4·13c43·13c1 | 19,007,345,500 | 2.9932 | 32:1
|
| 7-3-2-1 | 7 | 24·13c7·13c3·13c2·13c1 | 11,943,524,736 | 1.8808 | 52:1
|
| 6-4-3-0 | 7 | 24·13c6·13c4·13c3 | 8,421,716,160 | 1.3262 | 74:1
|
| 5-4-4-0 | 6 | 12·13c5·13c42 | 7,895,358,900 | 1.2433 | 79:1
|
| 5-5-3-0 | 7 | 12·13c52·13c3 | 5,684,658,408 | 0.8952 | 111:1
|
| 6-5-1-1 | 8 | 12·13c6·13c5·13c12 | 4,478,821,776 | 0.7053 | 141:1
|
| 6-5-2-0 | 9 | 24·13c6·13c5·13c2 | 4,134,297,024 | 0.6511 | 153:1
|
| 7-2-2-2 | 6 | 4·13c7·13c23 | 3,257,324,928 | 0.5130 | 194:1
|
| 7-4-1-1 | 8 | 12·13c7·13c4·13c12 | 2,488,234,320 | 0.3918 | 254:1
|
| 7-4-2-0 | 9 | 24·13c7·13c4·13c2 | 2,296,831,680 | 0.3617 | 275:1
|
| 7-3-3-0 | 8 | 12·13c7·13c32 | 1,684,343,232 | 0.2652 | 376:1
|
| 8-2-2-1 | 9 | 12·13c8·13c22·13c1 | 1,221,496,848 | 0.1924 | 519:1
|
| 8-3-1-1 | 9 | 12·13c8·13c3·13c12 | 746,470,296 | 0.1176 | 850:1
|
| 7-5-1-0 | 11 | 24·13c7·13c5·13c1 | 689,049,504 | 0.1085 | 921:1
|
| 8-3-2-0 | 10 | 24·13c8·13c3·13c2 | 689,049,504 | 0.1085 | 921:1
|
| 6-6-1-0 | 11 | 12·13c62·13c1 | 459,366,336 | 0.0723 | 1381:1
|
| 8-4-1-0 | 11 | 24·13c8·13c4·13c1 | 287,103,960 | 0.0452 | 2211:1
|
| 9-2-1-1 | 11 | 12·13c9·13c2·13c12 | 113,101,560 | 0.0178 | 5614:1
|
| 9-3-1-0 | 12 | 24·13c9·13c3·13c1 | 63,800,880 | 0.0100 | 9952:1
|
| 9-2-2-0 | 12 | 12·13c9·13c22 | 52,200,720 | 0.0082 | 12164:1
|
| 7-6-0-0 | 13 | 12·13c7·13c6 | 35,335,872 | 0.0056 | 17970:1
|
| 8-5-0-0 | 13 | 12·13c8·13c5 | 19,876,428 | 0.0031 | 31947:1
|
| 10-2-1-0 | 14 | 24·13c10·13c2·13c1 | 6,960,096 | 0.0011 | 91235:1
|
| 9-4-0-0 | 13 | 12·13c9·13c4 | 6,134,700 | 0.0010 | 103511:1
|
| 10-1-1-1 | 13 | 4·13c10·13c13 | 2,513,368 | 0.0004 | 252653:1
|
| 10-3-0-0 | 14 | 12·13c10·13c3 | 981,552 | 0.0002 | 646947:1
|
| 11-1-1-0 | 16 | 12·13c11·13c12 | 158,184 | 0.0000 | 4014397:1
|
| 11-2-0-0 | 16 | 12·13c11·13c2 | 73,008 | 0.0000 | 8697862:1
|
| 12-1-0-0 | 18 | 12·13c12·13c1 | 2028 | 0.0000 | 313123056:1
|
| 13-0-0-0 | 20 | 4·13c13 | 4 | 0.0000 | 158753389899:1
|
| Check totals: | 635,013,559,600 | 100 | |
The 39 generic patterns produce 560 specific patterns, which are listed below in order of frequency. (Only one entry is shown for each specific pattern because others would be the same except for suit identity.) The notation 4=4=3=2 means four spades, four hearts, three diamonds and two clubs; whereas 4-4-3-2 means any two four-card suits, any tripleton and any doubleton.
| Pattern | Freakness | Calculation | Hands | Percent | Odds Against
|
|---|
| 4=3=3=3 | 0 | 13c4·13c33 | 16,726,464,040 | 2.6340 | 37:1
|
| 4=4=3=2 | 1 | 13c42·13c3·13c2 | 11,404,407,300 | 1.7959 | 55:1
|
| 5=3=3=2 | 2 | 13c5·13c32·13c2 | 8,211,173,256 | 1.2931 | 76:1
|
| 5=4=2=2 | 3 | 13c5·13c4·13c22 | 5,598,527,220 | 0.8816 | 112:1
|
| 4=4=4=1 | 3 | 13c43·13c1 | 4,751,836,375 | 0.7483 | 133:1
|
| 5=4=3=1 | 4 | 13c5·13c4·13c3·13c1 | 3,421,322,190 | 0.5388 | 185:1
|
| 6=3=2=2 | 4 | 13c6·13c3·13c22 | 2,985,881,184 | 0.4702 | 212:1
|
| 6=3=3=1 | 5 | 13c6·13c32·13c1 | 1,824,705,168 | 0.2873 | 347:1
|
| 5=5=2=1 | 6 | 13c52·13c2·13c1 | 1,679,558,166 | 0.2645 | 377:1
|
| 6=4=2=1 | 6 | 13c6·13c4·13c2·13c1 | 1,244,117,160 | 0.1959 | 509:1
|
| 7=2=2=2 | 6 | 13c7·13c23 | 814,331,232 | 0.1282 | 779:1
|
| 5=4=4=0 | 6 | 13c5·13c42 | 657,946,575 | 0.1036 | 964:1
|
| 7=3=2=1 | 7 | 13c7·13c3·13c2·13c1 | 497,646,864 | 0.0784 | 1275:1
|
| 5=5=3=0 | 7 | 13c52·13c3 | 473,721,534 | 0.0746 | 1339:1
|
| 6=5=1=1 | 8 | 13c6·13c5·13c12 | 373,235,148 | 0.0588 | 1700:1
|
| 6=4=3=0 | 7 | 13c6·13c4·13c3 | 350,904,840 | 0.0553 | 1809:1
|
| 7=4=1=1 | 8 | 13c7·13c4·13c12 | 207,352,860 | 0.0327 | 3061:1
|
| 6=5=2=0 | 9 | 13c6·13c5·13c2 | 172,262,376 | 0.0271 | 3685:1
|
| 7=3=3=0 | 8 | 13c7·13c32 | 140,361,936 | 0.0221 | 4523:1
|
| 8=2=2=1 | 9 | 13c8·13c22·13c1 | 101,791,404 | 0.0160 | 6237:1
|
| 7=4=2=0 | 9 | 13c7·13c4·13c2 | 95,701,320 | 0.0151 | 6634:1
|
| 8=3=1=1 | 9 | 13c8·13c3·13c12 | 62,205,858 | 0.0098 | 10207:1
|
| 6=6=1=0 | 11 | 13c62·13c1 | 38,280,528 | 0.0060 | 16587:1
|
| 7=5=1=0 | 11 | 13c7·13c5·13c1 | 28,710,396 | 0.0045 | 22117:1
|
| 8=3=2=0 | 10 | 13c8·13c3·13c2 | 28,710,396 | 0.0045 | 22117:1
|
| 8=4=1=0 | 11 | 13c8·13c4·13c1 | 11,962,665 | 0.0019 | 53082:1
|
| 9=2=1=1 | 11 | 13c9·13c2·13c12 | 9,425,130 | 0.0015 | 67374:1
|
| 9=2=2=0 | 12 | 13c9·13c22 | 4,350,060 | 0.0007 | 145977:1
|
| 7=6=0=0 | 13 | 13c7·13c6 | 2,944,656 | 0.0005 | 215648:1
|
| 9=3=1=0 | 12 | 13c9·13c3·13c1 | 2,658,370 | 0.0004 | 238872:1
|
| 8=5=0=0 | 13 | 13c8·13c5 | 1,656,369 | 0.0003 | 383376:1
|
| 10=1=1=1 | 13 | 13c10·13c13 | 628,342 | 0.0001 | 1010617:1
|
| 9=4=0=0 | 13 | 13c9·13c4 | 511,225 | 0.0001 | 1242140:1
|
| 10=2=1=0 | 14 | 13c10·13c2·13c1 | 290,004 | 0.0000 | 2189671:1
|
| 10=3=0=0 | 14 | 13c10·13c3 | 81,796 | 0.0000 | 7763381:1
|
| 11=1=1=0 | 16 | 13c11·13c12 | 13,182 | 0.0000 | 48172777:1
|
| 11=2=0=0 | 16 | 13c11·13c2 | 6084 | 0.0000 | 104374351:1
|
| 12=1=0=0 | 18 | 13c12·13c1 | 169 | 0.0000 | 3757476683:1
|
| 13=0=0=0 | 20 | 13c13 | 1 | 0.0000 | 635013559599:1 |
Theoretical note: The above tables also apply to suit breaks among four hands. For example, the a priori chance of a suit splitting 4-4-3-2 is identical to that generic hand pattern; and the chance of a 4=4=3=2 split (say N=E=S=W) is identical to that specific hand pattern.
| Study 7Z77 Main |  | Top Against All Odds |
 Suit Lengths
Suit Lengths
This table lists cases pertaining to suit lengths. For example, the chance of being dealt at least 5-4 shape (any two suits) is shown to be about 37 percent, or 5-to-3 odds against.
The notation “6+ card suit” means at least a six-card suit.
| Hand Type | Calculation | Hands | Percent | Odds Against
|
|---|
| 13 card suit | 4·13c13=A | 4 | 0.0000 | 158753389899:1
|
| 12 card suit | 4·13c12·39c1=B | 2028 | 0.0000 | 313123056:1
|
| 11 card suit | 4·13c11·39c2=C | 231,192 | 0.0000 | 2746692:1
|
| 10 card suit | 4·13c10·39c3=D | 10,455,016 | 0.0016 | 60737:1
|
| 9 card suit | 4·13c9·39c4=E | 235,237,860 | 0.0370 | 2698:1
|
| 8 card suit | 4·13c8·39c5=F | 2,963,997,036 | 0.4668 | 213:1
|
| 7 card suit | 4·13c7·39c6=G | 22,394,644,272 | 3.5266 | 27:1
|
| 6 card suit (max) | 4·13c6(39c7-3·13c7-3·13c6·13c1)=H | 105,080,049,360 | 16.5477 | 5:1
|
| 5 card suit (max) | 4·13c5(39c8-3·13c8-3·13c7·26-3·13c6·26c2)-6·13c52·26c3=I | 281,562,853,572 | 44.3397 | 5:4
|
| 4 card suit (max) | 4·13c4·13c33+12·13c42·13c3·13c2+4·13c43·13c1=J | 222,766,089,260 | 35.0805 | 13:7
|
| 12+ card suit | A+B | 2032 | 0.0000 | 312506672:1
|
| 11+ card suit | A+B+C | 233,224 | 0.0000 | 2722761:1
|
| 10+ card suit | A+B+C+D | 10,688,240 | 0.0017 | 59411:1
|
| 9+ card suit | A+B+C+D+E | 245,926,100 | 0.0387 | 2581:1
|
| 8+ card suit | A+B+C+D+E+F | 3,209,923,136 | 0.5055 | 197:1
|
| 7+ card suit | A+B+C+D+E+F+G | 25,604,567,408 | 4.0321 | 24:1
|
| 6+ card suit | A+B+C+D+E+F+G+H | 130,684,616,768 | 20.5798 | 4:1
|
| 5+ card suit | A+B+C+D+E+F+G+H+I | 412,247,470,340 | 64.9195 | (favored)
|
| 4+ card suit | A+B+C+D+E+F+G+H+I+J | 635,013,559,600 | 100 | (bet on it)
|
| 9-4 two suits | 12·13c9·13c4=A | 6,134,700 | 0.0010 | 103511:1
|
| 8-5 two suits | 12·13c8·13c5=B | 19,876,428 | 0.0031 | 31947:1
|
| 8-4 two suits | 12·13c8·13c4·26c1=C | 287,103,960 | 0.0452 | 2211:1
|
| 7-6 two suits | 12·13c7·13c6=D | 35,335,872 | 0.0056 | 17970:1
|
| 7-5 two suits | 12·13c7·13c5·26c1=E | 689,049,504 | 0.1085 | 921:1
|
| 7-4 two suits | 12·13c7·13c4·26c2=F | 4,785,066,000 | 0.7535 | 132:1
|
| 6-6 two suits | 6·13c62·26c1=G | 459,366,336 | 0.0723 | 1381:1
|
| 6-5 two suits | 12·13c6·13c5·26c2=H | 8,613,118,800 | 1.3564 | 73:1
|
| 6-4 two suits | 12·13c6·13c4·26c3=I | 38,280,528,000 | 6.0283 | 16:1
|
| 5-5 two suits | 6·13c52·26c3=J | 25,839,356,400 | 4.0691 | 24:1
|
| 5-4 two suits | 12·13c5·13c4(26c4-13c4)=K | 157,189,418,100 | 24.7537 | 3:1
|
| 4-4 two suits (no 5) | 12·13c42·13c3·13c2+4·13c43·13c1=L | 155,860,233,100 | 24.5444 | 3:1
|
| At least 8-4 | A+B+C | 313,115,088 | 0.0493 | 2027:1
|
| At least 7-5 | B+D+E | 744,261,804 | 0.1172 | 852:1
|
| At least 7-4 | A+B+C+D+E+F | 5,822,566,464 | 0.9169 | 108:1
|
| At least 6-6 | D+G | 494,702,208 | 0.0779 | 1283:1
|
| At least 6-5 | B+D+G+H | 9,127,697,436 | 1.4374 | 69:1
|
| At least 6-4 | A+B+C+D+E+F+G+H+I | 53,175,579,600 | 8.3739 | 11:1
|
| At least 5-5 | B+D+E+G+H+J | 35,656,103,340 | 5.6150 | 17:1
|
| At least 5-4 | A+B+C+D+E+F+G+H+I+J+K | 236,204,354,100 | 37.1967 | 5:3
|
| At least 4-4 | A+B+C+D+E+F+G+H+I+J+K+L | 392,064,587,200 | 61.7411 | (favored)
|
| Three-suiter | 12·13c5·13c42+4·13c43·13c1=M | 26,902,704,400 | 4.2366 | 23:1
|
| Two-suiter (not 3) | A+B+C+D+E+F+G+H+I+J+K+L-M | 365,161,882,800 | 57.5046 | (favored) |
| Study 7Z77 Main |  | Top Against All Odds |
 Specific Cards
Specific Cards
The following 13 tables show the cases for any number of specific cards from 1 to 13. For example, to find the odds against holding all four aces, look at the table for “4 Cards” and the line “4 of 4” gives the answer as 378:1.
The notation “1+ of 4” means at least one of four.
| 1 Card | Calculation | Hands | Percent | Odds Against
|
|---|
| 1 of 1 | 1c1·51c12 | 158,753,389,900 | 25.0000 | 3:1
|
| 0 of 1 | 51c13 | 476,260,169,700 | 75.0000 | (favored) |
| 2 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 2 of 2 | 2c2·50c11=A | 37,353,738,800 | 5.8824 | 16:1
|
| 1 of 2 | 2c1·50c12=B | 242,799,302,200 | 38.2353 | 8:5
|
| 0 of 2 | 50c13 | 354,860,518,600 | 55.8824 | (favored)
|
| 1+ of 2 | A+B | 280,153,041,000 | 44.1176 | 5:4 |
| 3 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 3 of 3 | 3c3·49c10=A | 8,217,822,536 | 1.2941 | 76:1
|
| 2 of 3 | 3c2·49c11=B | 87,407,748,792 | 13.7647 | 6:1
|
| 1 of 3 | 3c1·49c12=C | 276,791,204,508 | 43.5882 | 5:4
|
| 0 of 3 | 49c13 | 262,596,783,764 | 41.3529 | 3:2
|
| 2+ of 3 | A+B | 95,625,571,328 | 15.0588 | 11:2
|
| 1+ of 3 | A+B+C | 372,416,775,836 | 58.6471 | (favored) |
| 4 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 4 of 4 | 4c4·48c9=A | 1,677,106,640 | 0.2641 | 378:1
|
| 3 of 4 | 4c3·48c10=B | 26,162,863,584 | 4.1200 | 23:1
|
| 2 of 4 | 4c2·48c11=C | 135,571,202,208 | 21.3493 | 4:1
|
| 1 of 4 | 4c1·48c12=D | 278,674,137,872 | 43.8848 | 5:4
|
| 0 of 4 | 48c13 | 192,928,249,296 | 30.3818 | 7:3
|
| 3+ of 4 | A+B | 27,839,970,224 | 4.3842 | 22:1
|
| 2+ of 4 | A+B+C | 163,411,172,432 | 25.7335 | 3:1
|
| 1+ of 4 | A+B+C+D | 442,085,310,304 | 69.6182 | (favored) |
| 5 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 5 of 5 | 5c5·47c8=A | 314,457,495 | 0.0495 | 2018:1
|
| 4 of 5 | 5c4·47c9=B | 6,813,245,725 | 1.0729 | 92:1
|
| 3 of 5 | 5c3·47c10=C | 51,780,667,510 | 8.1543 | 11:1
|
| 2 of 5 | 5c2·47c11=D | 174,171,336,170 | 27.4280 | 8:3
|
| 1 of 5 | 5c1·47c12=E | 261,257,004,255 | 41.1420 | 3:2
|
| 0 of 5 | 47c13 | 140,676,848,445 | 22.1534 | 7:2
|
| 4+ of 5 | A+B | 7,127,703,220 | 1.1224 | 88:1
|
| 3+ of 5 | A+B+C | 58,908,370,730 | 9.2767 | 10:1
|
| 2+ of 5 | A+B+C+D | 233,079,706,900 | 36.7047 | 5:3
|
| 1+ of 5 | A+B+C+D+E | 494,336,711,155 | 77.8466 | (favored) |
| 6 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 6 of 6 | 6c6·46c7=A | 53,524,680 | 0.0084 | 11863:1
|
| 5 of 6 | 6c5·46c8=B | 1,565,596,890 | 0.2465 | 405:1
|
| 4 of 6 | 6c4·46c9=C | 16,525,744,950 | 2.6024 | 37:1
|
| 3 of 6 | 6c3·46c10=D | 81,527,008,420 | 12.8386 | 13:2
|
| 2 of 6 | 6c2·46c11=E | 200,111,747,940 | 31.5130 | 2:1
|
| 1 of 6 | 6c1·46c12=F | 233,463,705,930 | 36.7652 | 5:3
|
| 0 of 6 | 46c13 | 101,766,230,790 | 16.0258 | 5:1
|
| 5+ of 6 | A+B | 1,619,121,570 | 0.2550 | 391:1
|
| 4+ of 6 | A+B+C | 18,144,866,520 | 2.8574 | 34:1
|
| 3+ of 6 | A+B+C+D | 99,671,874,940 | 15.6960 | 5:1
|
| 2+ of 6 | A+B+C+D+E | 299,783,622,880 | 47.2090 | 9:8
|
| 1+ of 6 | A+B+C+D+E+F | 533,247,328,810 | 83.9742 | (favored) |
| 7 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 7 of 7 | 7c7·45c6=A | 8,145,060 | 0.0013 | 77962:1
|
| 6 of 7 | 7c6·45c7=B | 317,657,340 | 0.0500 | 1998:1
|
| 5 of 7 | 7c5·45c8=C | 4,526,617,095 | 0.7128 | 139:1
|
| 4 of 7 | 7c4·45c9=D | 31,015,709,725 | 4.8843 | 19:1
|
| 3 of 7 | 7c3·45c10=E | 111,656,555,010 | 17.5833 | 9:2
|
| 2 of 7 | 7c2·45c11=F | 213,162,514,110 | 33.5682 | 2:1
|
| 1 of 7 | 7c1·45c12=G | 201,320,152,215 | 31.7033 | 2:1
|
| 0 of 7 | 45c13 | 73,006,209,045 | 11.4968 | 8:1
|
| 6+ of 7 | A+B | 325,802,400 | 0.0513 | 1948:1
|
| 5+ of 7 | A+B+C | 4,852,419,495 | 0.7641 | 130:1
|
| 4+ of 7 | A+B+C+D | 35,868,129,220 | 5.6484 | 17:1
|
| 3+ of 7 | A+B+C+D+E | 147,524,684,230 | 23.2317 | 7:2
|
| 2+ of 7 | A+B+C+D+E+F | 360,687,198,340 | 56.7999 | (favored)
|
| 1+ of 7 | A+B+C+D+E+F+G | 562,007,350,555 | 88.5032 | (favored) |
| 8 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 8 of 8 | 8c8·44c5=A | 1,086,008 | 0.0002 | 584722:1
|
| 7 of 8 | 8c7·44c6=B | 56,472,416 | 0.0089 | 11244:1
|
| 6 of 8 | 8c6·44c7=C | 1,072,975,904 | 0.1690 | 591:1
|
| 5 of 8 | 8c5·44c8=D | 9,925,027,112 | 1.5630 | 63:1
|
| 4 of 8 | 8c4·44c9=E | 49,625,135,560 | 7.8148 | 12:1
|
| 3 of 8 | 8c3·44c10=F | 138,950,379,568 | 21.8815 | 7:2
|
| 2 of 8 | 8c2·44c11=G | 214,741,495,696 | 33.8168 | 2:1
|
| 1 of 8 | 8c1·44c12=H | 168,725,460,904 | 26.5704 | 8:3
|
| 0 of 8 | 44c13 | 51,915,526,432 | 8.1755 | 11:1
|
| 7+ of 8 | A+B | 57,558,424 | 0.0091 | 11032:1
|
| 6+ of 8 | A+B+C | 1,130,534,328 | 0.1780 | 561:1
|
| 5+ of 8 | A+B+C+D | 11,055,561,440 | 1.7410 | 56:1
|
| 4+ of 8 | A+B+C+D+E | 60,680,697,000 | 9.5558 | 9:1
|
| 3+ of 8 | A+B+C+D+E+F | 199,631,076,568 | 31.4373 | 9:4
|
| 2+ of 8 | A+B+C+D+E+F+G | 414,372,572,264 | 65.2541 | (favored)
|
| 1+ of 8 | A+B+C+D+E+F+G+H | 583,098,033,168 | 91.8245 | (favored) |
| 9 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 9 of 9 | 9c9·43c4=A | 123,410 | 0.0000 | 5145559:1
|
| 8 of 9 | 9c8·43c5=B | 8,663,382 | 0.0014 | 73298:1
|
| 7 of 9 | 9c7·43c6=C | 219,472,344 | 0.0346 | 2892:1
|
| 6 of 9 | 9c6·43c7=D | 2,706,825,576 | 0.4263 | 234:1
|
| 5 of 9 | 9c5·43c8=E | 18,271,072,638 | 2.8773 | 34:1
|
| 4 of 9 | 9c4·43c9=F | 71,054,171,370 | 11.1894 | 8:1
|
| 3 of 9 | 9c3·43c10=G | 161,056,121,772 | 25.3626 | 3:1
|
| 2 of 9 | 9c2·43c11=H | 207,072,156,564 | 32.6091 | 2:1
|
| 1 of 9 | 9c1·43c12=I | 138,048,104,376 | 21.7394 | 7:2
|
| 0 of 9 | 43c13 | 36,576,848,168 | 5.7600 | 16:1
|
| 8+ of 9 | A+B | 8,786,792 | 0.0014 | 72268:1
|
| 7+ of 9 | A+B+C | 228,259,136 | 0.0359 | 2781:1
|
| 6+ of 9 | A+B+C+D | 2,935,084,712 | 0.4622 | 215:1
|
| 5+ of 9 | A+B+C+D+E | 21,206,157,350 | 3.3395 | 29:1
|
| 4+ of 9 | A+B+C+D+E+F | 92,260,328,720 | 14.5289 | 11:2
|
| 3+ of 9 | A+B+C+D+E+F+G | 253,316,450,492 | 39.8915 | 3:2
|
| 2+ of 9 | A+B+C+D+E+F+G+H | 460,388,607,056 | 72.5006 | (favored)
|
| 1+ of 9 | A+B+C+D+E+F+G+H+I | 598,436,711,432 | 94.2400 | (favored) |
| 10 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 10 of 10 | 10c10·42c3=A | 11,480 | 0.0000 | 55314769:1
|
| 9 of 10 | 10c9·42c4=B | 1,119,300 | 0.0002 | 567330:1
|
| 8 of 10 | 10c8·42c5=C | 38,280,060 | 0.0060 | 16588:1
|
| 7 of 10 | 10c7·42c6=D | 629,494,320 | 0.0991 | 1008:1
|
| 6 of 10 | 10c6·42c7=E | 5,665,448,880 | 0.8922 | 111:1
|
| 5 of 10 | 10c5·42c8=F | 29,743,606,620 | 4.6839 | 20:1
|
| 4 of 10 | 10c4·42c9=G | 93,637,280,100 | 14.7457 | 11:2
|
| 3 of 10 | 10c3·42c10=H | 176,573,156,760 | 27.8062 | 8:3
|
| 2 of 10 | 10c2·42c11=I | 192,625,261,920 | 30.3340 | 7:3
|
| 1 of 10 | 10c1·42c12=J | 110,581,168,880 | 17.4140 | 5:1
|
| 0 of 10 | 42c13 | 25,518,731,280 | 4.0186 | 24:1
|
| 9+ of 10 | A+B | 1,130,780 | 0.0002 | 561570:1
|
| 8+ of 10 | A+B+C | 39,410,840 | 0.0062 | 16112:1
|
| 7+ of 10 | A+B+C+D | 668,905,160 | 0.1053 | 948:1
|
| 6+ of 10 | A+B+C+D+E | 6,334,354,040 | 0.9975 | 99:1
|
| 5+ of 10 | A+B+C+D+E+F | 36,077,960,660 | 5.6814 | 17:1
|
| 4+ of 10 | A+B+C+D+E+F+G | 129,715,240,760 | 20.4272 | 4:1
|
| 3+ of 10 | A+B+C+D+E+F+G+H | 306,288,397,520 | 48.2334 | 13:12
|
| 2+ of 10 | A+B+C+D+E+F+G+H+I | 498,913,659,440 | 78.5674 | (favored)
|
| 1+ of 10 | A+B+C+D+E+F+G+H+I+J | 609,494,828,320 | 95.9814 | (favored) |
| 11 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 11 of 11 | 11c11·41c2=A | 820 | 0.0000 | 774406779:1
|
| 10 of 11 | 11c10·41c3=B | 117,260 | 0.0000 | 5415431:1
|
| 9 of 11 | 11c9·41c4=C | 5,569,850 | 0.0009 | 114008:1
|
| 8 of 11 | 11c8·41c5=D | 123,650,670 | 0.0195 | 5135:1
|
| 7 of 11 | 11c7·41c6=E | 1,483,808,040 | 0.2337 | 427:1
|
| 6 of 11 | 11c6·41c7=F | 10,386,656,280 | 1.6357 | 60:1
|
| 5 of 11 | 11c5·41c8=G | 44,143,289,190 | 6.9516 | 13:1
|
| 4 of 11 | 11c4·41c9=H | 115,613,376,450 | 18.2064 | 9:2
|
| 3 of 11 | 11c3·41c10=I | 184,981,402,320 | 29.1303 | 5:2
|
| 2 of 11 | 11c2·41c11=J | 173,770,408,240 | 27.3648 | 8:3
|
| 1 of 11 | 11c1·41c12=K | 86,885,204,120 | 13.6824 | 6:1
|
| 0 of 11 | 41c13 | 17,620,076,360 | 2.7748 | 35:1
|
| 10+ of 11 | A+B | 118,080 | 0.0000 | 5377824:1
|
| 9+ of 11 | A+B+C | 5,687,930 | 0.0009 | 111641:1
|
| 8+ of 11 | A+B+C+D | 129,338,600 | 0.0204 | 4909:1
|
| 7+ of 11 | A+B+C+D+E | 1,613,146,640 | 0.2540 | 393:1
|
| 6+ of 11 | A+B+C+D+E+F | 11,999,802,920 | 1.8897 | 52:1
|
| 5+ of 11 | A+B+C+D+E+F+G | 56,143,092,110 | 8.8412 | 10:1
|
| 4+ of 11 | A+B+C+D+E+F+G+H | 171,756,468,560 | 27.0477 | 8:3
|
| 3+ of 11 | A+B+C+D+E+F+G+H+I | 356,737,870,880 | 56.1780 | (favored)
|
| 2+ of 11 | A+B+C+D+E+F+G+H+I+J | 530,508,279,120 | 83.5428 | (favored)
|
| 1+ of 11 | A+B+C+D+E+F+G+H+I+J+K | 617,393,483,240 | 97.2252 | (favored) |
| 12 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 12 of 12 | 12c12·40c1=A | 40 | 0.0000 | 15875338989:1
|
| 11 of 12 | 12c11·40c2=B | 9360 | 0.0000 | 67843328:1
|
| 10 of 12 | 12c10·40c3=C | 652,080 | 0.0001 | 973827:1
|
| 9 of 12 | 12c9·40c4=D | 20,105,800 | 0.0032 | 31583:1
|
| 8 of 12 | 12c8·40c5=E | 325,713,960 | 0.0513 | 1949:1
|
| 7 of 12 | 12c7·40c6=F | 3,039,996,960 | 0.4787 | 208:1
|
| 6 of 12 | 12c6·40c7=G | 17,226,649,440 | 2.7128 | 36:1
|
| 5 of 12 | 12c5·40c8=H | 60,908,510,520 | 9.5917 | 9:1
|
| 4 of 12 | 12c4·40c9=I | 135,352,245,600 | 21.3149 | 4:1
|
| 3 of 12 | 12c3·40c10=J | 186,485,316,160 | 29.3671 | 5:2
|
| 2 of 12 | 12c2·40c11=K | 152,578,895,040 | 24.0277 | 3:1
|
| 1 of 12 | 12c1·40c12=L | 67,042,241,760 | 10.5576 | 8:1
|
| 0 of 12 | 40c13 | 12,033,222,880 | 1.8950 | 52:1
|
| 11+ of 12 | A+B | 9400 | 0.0000 | 67554633:1
|
| 10+ of 12 | A+B+C | 661,480 | 0.0001 | 959988:1
|
| 9+ of 12 | A+B+C+D | 20,767,280 | 0.0033 | 30577:1
|
| 8+ of 12 | A+B+C+D+E | 346,481,240 | 0.0546 | 1832:1
|
| 7+ of 12 | A+B+C+D+E+F | 3,386,478,200 | 0.5333 | 187:1
|
| 6+ of 12 | A+B+C+D+E+F+G | 20,613,127,640 | 3.2461 | 30:1
|
| 5+ of 12 | A+B+C+D+E+F+G+H | 81,521,638,160 | 12.8378 | 13:2
|
| 4+ of 12 | A+B+C+D+E+F+G+H+I | 216,873,883,760 | 34.1526 | 2:1
|
| 3+ of 12 | A+B+C+D+E+F+G+H+I+J | 403,359,199,920 | 63.5198 | (favored)
|
| 2+ of 12 | A+B+C+D+E+F+G+H+I+J+K | 555,938,094,960 | 87.5474 | (favored)
|
| 1+ of 12 | A+B+C+D+E+F+G+H+I+J+K+L | 622,980,336,720 | 98.1050 | (favored) |
| 13 Cards | Calculation | Hands | Percent | Odds Against
|
|---|
| 13 of 13 | 13c13=A | 1 | 0.0000 | 635013559599:1
|
| 12 of 13 | 13c12·39c1=B | 507 | 0.0000 | 1252492227:1
|
| 11 of 13 | 13c11·39c2=C | 57,798 | 0.0000 | 10986773:1
|
| 10 of 13 | 13c10·39c3=D | 2,613,754 | 0.0004 | 242950:1
|
| 9 of 13 | 13c9·39c4=E | 58,809,465 | 0.0093 | 10797:1
|
| 8 of 13 | 13c8·39c5=F | 740,999,259 | 0.1167 | 856:1
|
| 7 of 13 | 13c7·39c6=G | 5,598,661,068 | 0.8817 | 112:1
|
| 6 of 13 | 13c6·39c7=H | 26,393,687,892 | 4.1564 | 23:1
|
| 5 of 13 | 13c5·39c8=I | 79,181,063,676 | 12.4692 | 7:1
|
| 4 of 13 | 13c4·39c9=J | 151,519,319,380 | 23.8608 | 3:1
|
| 3 of 13 | 13c3·39c10=K | 181,823,183,256 | 28.6330 | 5:2
|
| 2 of 13 | 13c2·39c11=L | 130,732,371,432 | 20.5873 | 4:1
|
| 1 of 13 | 13c1·39c12=M | 50,840,366,668 | 8.0062 | 11:1
|
| 0 of 13 | 39c13 | 8,122,425,444 | 1.2791 | 77:1
|
| 12+ of 13 | A+B | 508 | 0.0000 | 1250026691:1
|
| 11+ of 13 | A+B+C | 58,306 | 0.0000 | 10891049:1
|
| 10+ of 13 | A+B+C+D | 2,672,060 | 0.0004 | 237648:1
|
| 9+ of 13 | A+B+C+D+E | 61,481,525 | 0.0097 | 10328:1
|
| 8+ of 13 | A+B+C+D+E+F | 802,480,784 | 0.1264 | 790:1
|
| 7+ of 13 | A+B+C+D+E+F+G | 6,401,141,852 | 1.0080 | 98:1
|
| 6+ of 13 | A+B+C+D+E+F+G+H | 32,794,829,744 | 5.1644 | 18:1
|
| 5+ of 13 | A+B+C+D+E+F+G+H+I | 111,975,893,420 | 17.6336 | 9:2
|
| 4+ of 13 | A+B+C+D+E+F+G+H+I+J | 263,495,212,800 | 41.4944 | 3:2
|
| 3+ of 13 | A+B+C+D+E+F+G+H+I+J+K | 445,318,396,056 | 70.1274 | (favored)
|
| 2+ of 13 | A+B+C+D+E+F+G+H+I+J+K+L | 576,050,767,488 | 90.7147 | (favored)
|
| 1+ of 13 | A+B+C+D+E+F+G+H+I+J+K+L+M | 626,891,134,156 | 98.7209 | (favored) |
| Study 7Z77 Main |  | Top Against All Odds |
© 2003 Richard Pavlicek

 by Richard Pavlicek
by Richard Pavlicek by Richard Pavlicek
by Richard Pavlicek *Combinatorial notation (NcR) is frequently used. Think of this as “N choose R” which means, given N items, the number of ways to select R of them. For example, 26c2 means “26 choose 2” which can be done in 325 ways; I could have just use the number 325, but the notation is more meaningful to show how the number is derived.
*Combinatorial notation (NcR) is frequently used. Think of this as “N choose R” which means, given N items, the number of ways to select R of them. For example, 26c2 means “26 choose 2” which can be done in 325 ways; I could have just use the number 325, but the notation is more meaningful to show how the number is derived.
 General Criteria
General Criteria A-K
A-K  A-K-Q-J-10-9-2
A-K-Q-J-10-9-2  A-K-Q
A-K-Q 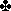 A, but note that changing the
A, but note that changing the  9 to the eight would disqualify it.
9 to the eight would disqualify it.

 Hand Patterns
Hand Patterns
 Suit Lengths
Suit Lengths
 Specific Cards
Specific Cards