Study 8J37 Main

Hits and Misses

by Richard Pavlicek

Bridge players are a strange breed. Besides their addiction to this great card game, many enjoy looking for bizarre characteristics in a bridge hand. This study — a wasted effort in productivity if there ever was one — will analyze some of these quirks.

Magnus Hits

Symmetric Suits

Straight Flushes

Unique Ranks

Alphabetic Suits

I may occasionally add to this stupidity, I mean study, so if you have a favorite diversion, pass it along.

Magnus Hits

Magnus Olafsson of New York City (originally Iceland) enjoys looking for suits in which the lowest card describes the suit length. For example, K-J-7-4 qualifies because the lowest card is a four in a four-card suit. A bridge hand can have as many as four hits, e.g., A-Q-9-7-5 8-6-3 K-10-3 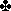J-2, where the lowest cards in each suit identify the 5=3=3=2 shape.

Of the 8192 possible suit holdings, only 377 qualify as Magnus hits. The longest suit to qualify is seven cards, i.e., A-K-Q-J-10-9-7 is one of seven possible holdings. Obviously an eight-card suit could not have the eight as its lowest card.

A singleton qualifies only if it’s the ace, which is arbitrarily considered “one” to meet the rule. A void also qualifies, because having “no lowest card” matches having “no cards” — or at least we’ll take Magnus’s word for it. Reminds me of being told by my math teacher for the first time that “zero factorial equals 1.” I thought he had lost his marbles.

The following table shows the percent chance of each number of Magnus hits for each generic hand pattern. Hit percents are relative to the generic pattern in that row. Total percents (last column) are relative to all bridge hands. The bottom row shows the percents for all generic patterns combined. Percents shown as 0.0000 are not zero but round that way to the nearest 10,000th.

Percents for Magnus Hits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	47.3279	38.9639	11.9901	1.6348	0.0833	21.5512
5-3-3-2	49.7961	38.1705	10.6903	1.2875	0.0557	15.5168
5-4-3-1	55.9691	35.3521	7.9162	0.7382	0.0243	12.9307
5-4-2-2	53.7481	36.2179	9.0162	0.9790	0.0389	10.5797
4-3-3-3	43.8479	40.1632	13.7737	2.0958	0.1194	10.5361
6-3-2-2	55.9417	35.5491	7.8283	0.6661	0.0149	5.6425
6-4-2-1	62.8766	31.4740	5.3053	0.3377	0.0065	4.7021
6-3-3-1	58.2533	34.5593	6.7135	0.4646	0.0093	3.4482
5-5-2-1	63.5616	30.6498	5.3698	0.4075	0.0113	3.1739
4-4-4-1	53.1950	36.6181	9.1732	0.9773	0.0364	2.9932
7-3-2-1	62.8287	31.8757	5.0479	0.2468	0.0009	1.8808
6-4-3-0	0	65.0201	30.7877	4.0868	0.1053	1.3262
5-4-4-0	0	62.4706	31.9780	5.2757	0.2758	1.2433
5-5-3-0	0	65.7284	29.9163	4.1710	0.1843	0.8952
6-5-1-1	74.3567	22.9709	2.5516	0.1188	0.0019	0.7053
6-5-2-0	0	73.8404	23.9302	2.1803	0.0492	0.6511
7-2-2-2	60.3355	33.1574	6.1185	0.3872	0.0015	0.5130
7-4-1-1	70.6174	26.3010	2.9706	0.1106	0.0004	0.3918
7-4-2-0	0	70.1270	27.1808	2.6817	0.0105	0.3617
7-3-3-0	0	64.9706	31.2045	3.8099	0.0151	0.2652
8-2-2-1	66.0901	29.5403	4.1875	0.1821	0	0.1924
8-3-1-1	68.8211	27.8562	3.2089	0.1138	0	0.1176
7-5-1-0	0	82.9309	16.2508	0.8152	0.0031	0.1085
8-3-2-0	0	68.3432	28.6982	2.9586	0	0.1085
6-6-1-0	0	86.3813	13.0266	0.5840	0.0082	0.0723
8-4-1-0	0	76.8155	21.8935	1.2910	0	0.0452
9-2-1-1	72.0983	25.1252	2.6855	0.0910	0	0.0178
9-3-1-0	0	74.5562	23.9645	1.4793	0	0.0100
9-2-2-0	0	71.5976	26.0355	2.3669	0	0.0082
7-6-0-0	0	0	96.3420	3.6447	0.0133	0.0056
8-5-0-0	0	0	90.2098	9.7902	0	0.0031
10-2-1-0	0	78.1065	20.7101	1.1834	0	0.0011
9-4-0-0	0	0	83.2168	16.7832	0	0.0010
10-1-1-1	78.6527	19.6632	1.6386	0.0455	0	0.0004
10-3-0-0	0	0	80.7692	19.2308	0	0.0002
11-1-1-0	0	85.2071	14.2012	0.5917	0	0.0000
11-2-0-0	0	0	84.6154	15.3846	0	0.0000
12-1-0-0	0	0	92.3077	7.6923	0	0.0000
13-0-0-0	0	0	0	100	0	0.0000
All 39	49.7148	38.2396	10.7001	1.2893	0.0563	100

Exact Hand Counts for Magnus Hits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	64,769,581,800	53,323,162,200	16,408,854,000	2,237,241,600	114,048,000	136,852,887,600
5-3-3-2	49,066,079,832	37,610,906,256	10,533,565,944	1,268,641,440	54,885,600	98,534,079,072
5-4-3-1	45,957,209,760	29,028,245,400	6,500,130,120	606,188,880	19,958,400	82,111,732,560
5-4-2-2	36,109,236,240	24,331,998,240	6,057,270,720	657,694,080	26,127,360	67,182,326,640
4-3-3-3	29,336,810,580	26,871,532,380	9,215,444,700	1,402,208,500	79,860,000	66,905,856,160
6-3-2-2	20,044,221,120	12,737,431,872	2,804,934,528	238,664,448	5,322,240	35,830,574,208
6-4-2-1	18,774,201,600	9,397,748,160	1,584,092,160	100,834,560	1,935,360	29,858,811,840
6-3-3-1	12,755,413,440	7,567,260,624	1,470,028,032	101,727,120	2,032,800	21,896,462,016
5-5-2-1	12,810,641,184	6,177,365,208	1,082,267,568	82,137,888	2,286,144	20,154,697,992
4-4-4-1	10,110,954,000	6,960,131,500	1,743,588,000	185,760,000	6,912,000	19,007,345,500
7-3-2-1	7,503,959,232	3,807,079,056	602,898,912	29,476,656	110,880	11,943,524,736
6-4-3-0	0	5,475,808,800	2,592,854,880	344,182,080	8,870,400	8,421,716,160
5-4-4-0	0	4,932,276,300	2,524,775,400	416,534,400	21,772,800	7,895,358,900
5-5-3-0	0	3,736,437,012	1,700,637,444	237,105,792	10,478,160	5,684,658,408
6-5-1-1	3,330,305,280	1,028,827,008	114,282,576	5,322,240	84,672	4,478,821,776
6-5-2-0	0	3,052,779,840	989,345,664	90,139,392	2,032,128	4,134,297,024
7-2-2-2	1,965,322,656	1,080,044,064	199,298,880	12,610,944	48,384	3,257,324,928
7-4-1-1	1,757,125,440	654,429,600	73,916,340	2,752,860	10,080	2,488,234,320
7-4-2-0	0	1,610,698,320	624,298,320	61,593,120	241,920	2,296,831,680
7-3-3-0	0	1,094,327,388	525,590,604	64,171,140	254,100	1,684,343,232
8-2-2-1	807,288,768	360,833,616	51,150,528	2,223,936	0	1,221,496,848
8-3-1-1	513,729,216	207,938,016	23,953,644	849,420	0	746,470,296
7-5-1-0	0	571,434,912	111,976,344	5,617,080	21,168	689,049,504
8-3-2-0	0	470,918,448	197,744,976	20,386,080	0	689,049,504
6-6-1-0	0	396,806,400	59,839,680	2,682,624	37,632	459,366,336
8-4-1-0	0	220,540,320	62,857,080	3,706,560	0	287,103,960
9-2-1-1	81,544,320	28,416,960	3,037,320	102,960	0	113,101,560
9-3-1-0	0	47,567,520	15,289,560	943,800	0	63,800,880
9-2-2-0	0	37,374,480	13,590,720	1,235,520	0	52,200,720
7-6-0-0	0	0	34,043,280	1,287,888	4704	35,335,872
8-5-0-0	0	0	17,930,484	1,945,944	0	19,876,428
10-2-1-0	0	5,436,288	1,441,440	82,368	0	6,960,096
9-4-0-0	0	0	5,105,100	1,029,600	0	6,134,700
10-1-1-1	1,976,832	494,208	41,184	1144	0	2,513,368
10-3-0-0	0	0	792,792	188,760	0	981,552
11-1-1-0	0	134,784	22,464	936	0	158,184
11-2-0-0	0	0	61,776	11,232	0	73,008
12-1-0-0	0	0	1872	156	0	2028
13-0-0-0	0	0	0	4	0	4
All 39	315,695,601,300	242,826,385,180	67,946,955,036	8,187,283,152	357,334,932	635,013,559,600

Study 8J37 Main

Top Hits and Misses

Symmetric Suits

Peter Boyd of Darnestown, Maryland — one of the truly great players and a former world champion — enjoys looking for suits that are symmetric. That is, the rank differentials remain the same if the suit is turned upside-down. For example, A-K-3-2 has the two highest and two lowest cards, so flipping would not change it. Other examples are Q-4, J-8-5, K-J-5-3 and A-Q-8-4-2.

Of the 8192 possible suit holdings, only 128 are symmetric. Any odd-length symmetric suit must contain the eight, the middle card. Hence the only singleton to qualify is a singleton eight. A void suit certainly qualifies: Turning a void upside-down wouldn’t change it — or if it did, Penn and Teller might have a new act.

The following table shows the percent chance of each number of symmetric hits for each generic hand pattern. Hit percents are relative to the generic pattern in that row. Total percents (last column) are relative to all bridge hands. The bottom row shows the percents for all generic patterns combined. Percents shown as 0.0000 are not zero but round that way to the nearest 10,000th.

Percents for Symmetric Suits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	86.6191	12.7866	0.5834	0.0108	0.0001	21.5512
5-3-3-2	87.4441	12.0658	0.4826	0.0075	0.0000	15.5168
5-4-3-1	87.4441	12.0658	0.4826	0.0075	0.0000	12.9307
5-4-2-2	82.4473	16.4802	1.0499	0.0225	0.0001	10.5797
4-3-3-3	91.8688	7.8745	0.2531	0.0036	0.0000	10.5361
6-3-2-2	82.4473	16.4802	1.0499	0.0225	0.0001	5.6425
6-4-2-1	82.4473	16.4802	1.0499	0.0225	0.0001	4.7021
6-3-3-1	87.4441	12.0658	0.4826	0.0075	0.0000	3.4482
5-5-2-1	83.2325	15.8351	0.9167	0.0156	0.0001	3.1739
4-4-4-1	86.6191	12.7866	0.5834	0.0108	0.0001	2.9932
7-3-2-1	82.4473	16.4802	1.0499	0.0225	0.0001	1.8808
6-4-3-0	0	94.7311	5.1770	0.0914	0.0005	1.3262
5-4-4-0	0	94.7311	5.1770	0.0914	0.0005	1.2433
5-5-3-0	0	95.6333	4.3048	0.0616	0.0003	0.8952
6-5-1-1	83.2325	15.8351	0.9167	0.0156	0.0001	0.7053
6-5-2-0	0	90.1685	9.6407	0.1898	0.0010	0.6511
7-2-2-2	77.7360	20.3507	1.8487	0.0641	0.0005	0.5130
7-4-1-1	82.4473	16.4802	1.0499	0.0225	0.0001	0.3918
7-4-2-0	0	89.3179	10.4104	0.2698	0.0019	0.3617
7-3-3-0	0	94.7311	5.1770	0.0914	0.0005	0.2652
8-2-2-1	77.7360	20.3507	1.8487	0.0641	0.0005	0.1924
8-3-1-1	82.4473	16.4802	1.0499	0.0225	0.0001	0.1176
7-5-1-0	0	90.1685	9.6407	0.1898	0.0010	0.1085
8-3-2-0	0	89.3179	10.4104	0.2698	0.0019	0.1085
6-6-1-0	0	90.1685	9.6407	0.1898	0.0010	0.0723
8-4-1-0	0	89.3179	10.4104	0.2698	0.0019	0.0452
9-2-1-1	77.0027	20.9007	2.0167	0.0789	0.0010	0.0178
9-3-1-0	0	88.4753	11.1647	0.3566	0.0034	0.0100
9-2-2-0	0	83.4195	15.6908	0.8772	0.0124	0.0082
7-6-0-0	0	0	97.6826	2.3038	0.0136	0.0056
8-5-0-0	0	0	97.6826	2.3038	0.0136	0.0031
A-2-1-0	0	83.4195	15.6908	0.8772	0.0124	0.0011
9-4-0-0	0	0	95.8482	4.1078	0.0440	0.0010
10-1-1-1	77.0027	20.9007	2.0167	0.0789	0.0010	0.0004
10-3-0-0	0	0	95.8482	4.1078	0.0440	0.0002
11-1-1-0	0	78.6527	19.6632	1.6386	0.0455	0.0000
11-2-0-0	0	0	85.2071	14.2012	0.5917	0.0000
12-1-0-0	0	0	85.2071	14.2012	0.5917	0.0000
13-0-0-0	0	0	0	0	100	0.0000
All 39	81.8437	17.1891	0.9488	0.0182	0.0001	100

Exact Hand Counts for Symmetric Suits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	118,540,800,000	17,498,880,000	798,336,000	14,774,400	97,200	136,852,887,600
5-3-3-2	86,162,227,200	11,888,916,480	475,504,128	7,392,384	38,880	98,534,079,072
5-4-3-1	71,801,856,000	9,907,430,400	396,253,440	6,160,320	32,400	82,111,732,560
5-4-2-2	55,390,003,200	11,071,779,840	705,335,040	15,111,360	97,200	67,182,326,640
4-3-3-3	61,465,600,000	5,268,480,000	169,344,000	2,419,200	12,960	66,905,856,160
6-3-2-2	29,541,335,040	5,904,949,248	376,178,688	8,059,392	51,840	35,830,574,208
6-4-2-1	24,617,779,200	4,920,791,040	313,482,240	6,716,160	43,200	29,858,811,840
6-3-3-1	19,147,161,600	2,641,981,440	105,667,584	1,642,752	8640	21,896,462,016
5-5-2-1	16,775,258,112	3,191,519,232	184,768,128	3,136,320	16,200	20,154,697,992
4-4-4-1	16,464,000,000	2,430,400,000	110,880,000	2,052,000	13,500	19,007,345,500
7-3-2-1	9,847,111,680	1,968,316,416	125,392,896	2,686,464	17,280	11,943,524,736
6-4-3-0	0	7,977,984,000	435,993,600	7,695,360	43,200	8,421,716,160
5-4-4-0	0	7,479,360,000	408,744,000	7,214,400	40,500	7,895,358,900
5-5-3-0	0	5,436,426,240	244,712,448	3,503,520	16,200	5,684,658,408
6-5-1-1	3,727,835,136	709,226,496	41,059,584	696,960	3600	4,478,821,776
6-5-2-0	0	3,727,835,136	398,573,568	7,845,120	43,200	4,134,297,024
7-2-2-2	2,532,114,432	662,888,448	60,217,344	2,087,424	17,280	3,257,324,928
7-4-1-1	2,051,481,600	410,065,920	26,123,520	559,680	3600	2,488,234,320
7-4-2-0	0	2,051,481,600	239,109,120	6,197,760	43,200	2,296,831,680
7-3-3-0	0	1,595,596,800	87,198,720	1,539,072	8640	1,684,343,232
8-2-2-1	949,542,912	248,583,168	22,581,504	782,784	6480	1,221,496,848
8-3-1-1	615,444,480	123,019,776	7,837,056	167,904	1080	746,470,296
7-5-1-0	0	621,305,856	66,428,928	1,307,520	7200	689,049,504
8-3-2-0	0	615,444,480	71,732,736	1,859,328	12,960	689,049,504
6-6-1-0	0	414,203,904	44,285,952	871,680	4800	459,366,336
8-4-1-0	0	256,435,200	29,888,640	774,720	5400	287,103,960
9-2-1-1	87,091,200	23,639,040	2,280,960	89,280	1080	113,101,560
9-3-1-0	0	56,448,000	7,123,200	227,520	2160	63,800,880
9-2-2-0	0	43,545,600	8,190,720	457,920	6480	52,200,720
7-6-0-0	0	0	34,516,992	814,080	4800	35,335,872
8-5-0-0	0	0	19,415,808	457,920	2700	19,876,428
10-2-1-0	0	5,806,080	1,092,096	61,056	864	6,960,096
9-4-0-0	0	0	5,880,000	252,000	2700	6,134,700
10-1-1-1	1,935,360	525,312	50,688	1984	24	2,513,368
10-3-0-0	0	0	940,800	40,320	432	981,552
11-1-1-0	0	124,416	31,104	2592	72	158,184
11-2-0-0	0	0	62,208	10,368	432	73,008
12-1-0-0	0	0	1728	288	12	2028
13-0-0-0	0	0	0	0	4	4
All 39	519,718,577,152	109,153,389,568	6,025,215,168	115,669,312	708,400	635,013,559,600

Study 8J37 Main

Top Hits and Misses

Straight Flushes

Jeff Bayone of New York City, owner-manager of Honors Bridge Club and author of “A Taste of Bridge,” enjoys a taste of poker instead, looking for straight flushes. I’m not sure I like this, because every time you find one, it means you’re playing the wrong game, wasting at bridge what could have won big-time at the poker table. Oh well, to each his own.

Of the 8192 possible suit holdings, 1378 contain at least one straight flush, which of course requires at least a five-card suit. Multiple occurrences are possible in the same suit, or in either of two suits. I will assume a liberal view allowing cards to be used more than once, so K-Q-J-10-9-8-7 contains three straight flushes; and A-6-5-4-3-2 contains two, since the ace can be low in poker. Indeed, a 13-card suit has 10 straight flushes!

The following table shows the percent chance of each number of straight-flush hits for each generic hand pattern. Hit percents are relative to the generic pattern in that row. Total percents (last column) are relative to all bridge hands. The bottom row shows the percents for all generic patterns combined. Percents shown as 0.0000 are not zero but round that way to the nearest 10,000th.

Percents for Straight Flushes

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4+ Hits	Total
4-4-3-2	100	0	0	0	0	21.5512
5-3-3-2	99.2230	0.7770	0	0	0	15.5168
5-4-3-1	99.2230	0.7770	0	0	0	12.9307
5-4-2-2	99.2230	0.7770	0	0	0	10.5797
4-3-3-3	100	0	0	0	0	10.5361
6-3-2-2	95.8625	3.6131	0.5245	0	0	5.6425
6-4-2-1	95.8625	3.6131	0.5245	0	0	4.7021
6-3-3-1	95.8625	3.6131	0.5245	0	0	3.4482
5-5-2-1	98.4520	1.5419	0.0060	0	0	3.1739
4-4-4-1	100	0	0	0	0	2.9932
7-3-2-1	87.3543	9.4406	2.7389	0.4662	0	1.8808
6-4-3-0	95.8625	3.6131	0.5245	0	0	1.3262
5-4-4-0	99.2230	0.7770	0	0	0	1.2433
5-5-3-0	98.4520	1.5419	0.0060	0	0	0.8952
6-5-1-1	95.1176	4.3298	0.5485	0.0041	0	0.7053
6-5-2-0	95.1176	4.3298	0.5485	0.0041	0	0.6511
7-2-2-2	87.3543	9.4406	2.7389	0.4662	0	0.5130
7-4-1-1	87.3543	9.4406	2.7389	0.4662	0	0.3918
7-4-2-0	87.3543	9.4406	2.7389	0.4662	0	0.3617
7-3-3-0	87.3543	9.4406	2.7389	0.4662	0	0.2652
8-2-2-1	71.1733	17.8710	7.7700	2.6418	0.5439	0.1924
8-3-1-1	71.1733	17.8710	7.7700	2.6418	0.5439	0.1176
7-5-1-0	86.6756	10.0459	2.7910	0.4839	0.0036	0.1085
8-3-2-0	71.1733	17.8710	7.7700	2.6418	0.5439	0.1085
6-6-1-0	91.8961	6.9271	1.1361	0.0379	0.0028	0.0723
8-4-1-0	71.1733	17.8710	7.7700	2.6418	0.5439	0.0452
9-2-1-1	46.2937	26.2937	15.5245	7.8322	4.0559	0.0178
9-3-1-0	46.2937	26.2937	15.5245	7.8322	4.0559	0.0100
9-2-2-0	46.2937	26.2937	15.5245	7.8322	4.0559	0.0082
7-6-0-0	83.7400	12.2061	3.4248	0.5954	0.0337	0.0056
8-5-0-0	70.6203	18.2852	7.8485	2.6816	0.5644	0.0031
10-2-1-0	18.1818	24.4755	25.1748	16.0839	16.0839	0.0011
9-4-0-0	46.2937	26.2937	15.5245	7.8322	4.0559	0.0010
10-1-1-1	18.1818	24.4755	25.1748	16.0839	16.0839	0.0004
10-3-0-0	18.1818	24.4755	25.1748	16.0839	16.0839	0.0002
11-1-1-0	1.2821	7.6923	15.3846	28.2051	47.4359	0.0000
11-2-0-0	1.2821	7.6923	15.3846	28.2051	47.4359	0.0000
12-1-0-0	0	0	0	0	100	0.0000
13-0-0-0	0	0	0	0	100	0.0000
All 39	98.3237	1.4130	0.2269	0.0321	0.0043	100

Exact Hand Counts for Straight Flushes

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4+ Hits	Total
4-4-3-2	136,852,887,600	0	0	0	0	136,852,887,600
5-3-3-2	97,768,468,512	765,610,560	0	0	0	98,534,079,072
5-4-3-1	81,473,723,760	638,008,800	0	0	0	82,111,732,560
5-4-2-2	66,660,319,440	522,007,200	0	0	0	67,182,326,640
4-3-3-3	66,905,856,160	0	0	0	0	66,905,856,160
6-3-2-2	34,348,073,760	1,294,577,856	187,922,592	0	0	35,830,574,208
6-4-2-1	28,623,394,800	1,078,814,880	156,602,160	0	0	29,858,811,840
6-3-3-1	20,990,489,520	791,130,912	114,841,584	0	0	21,896,462,016
5-5-2-1	19,842,710,472	310,770,720	1,216,800	0	0	20,154,697,992
4-4-4-1	19,007,345,500	0	0	0	0	19,007,345,500
7-3-2-1	10,433,183,904	1,127,535,552	327,124,512	55,680,768	0	11,943,524,736
6-4-3-0	8,073,265,200	304,281,120	44,169,840	0	0	8,421,716,160
5-4-4-0	7,834,011,900	61,347,000	0	0	0	7,895,358,900
5-5-3-0	5,596,661,928	87,653,280	343,200	0	0	5,684,658,408
6-5-1-1	4,260,148,620	193,925,472	24,565,164	182,520	0	4,478,821,776
6-5-2-0	3,932,444,880	179,008,128	22,675,536	168,480	0	4,134,297,024
7-2-2-2	2,845,413,792	307,509,696	89,215,776	15,185,664	0	3,257,324,928
7-4-1-1	2,173,579,980	234,903,240	68,150,940	11,600,160	0	2,488,234,320
7-4-2-0	2,006,381,520	216,833,760	62,908,560	10,707,840	0	2,296,831,680
7-3-3-0	1,471,346,448	159,011,424	46,132,944	7,852,416	0	1,684,343,232
8-2-2-1	869,379,264	218,293,920	94,910,400	32,269,536	6,643,728	1,221,496,848
8-3-1-1	531,287,328	133,401,840	58,000,800	19,720,272	4,060,056	746,470,296
7-5-1-0	597,237,576	69,221,568	19,231,368	3,334,032	24,960	689,049,504
8-3-2-0	490,419,072	123,140,160	53,539,200	18,203,328	3,747,744	689,049,504
6-6-1-0	422,139,900	31,820,880	5,218,824	174,096	12,636	459,366,336
8-4-1-0	204,341,280	51,308,400	22,308,000	7,584,720	1,561,560	287,103,960
9-2-1-1	52,358,904	29,738,592	17,558,424	8,858,304	4,587,336	113,101,560
9-3-1-0	29,535,792	16,775,616	9,904,752	4,996,992	2,587,728	63,800,880
9-2-2-0	24,165,648	13,725,504	8,103,888	4,088,448	2,117,232	52,200,720
7-6-0-0	29,590,260	4,313,136	1,210,200	210,384	11,892	35,335,872
8-5-0-0	14,036,784	3,634,440	1,560,000	533,016	112,188	19,876,428
10-2-1-0	1,265,472	1,703,520	1,752,192	1,119,456	1,119,456	6,960,096
9-4-0-0	2,839,980	1,613,040	952,380	480,480	248,820	6,134,700
10-1-1-1	456,976	615,160	632,736	404,248	404,248	2,513,368
10-3-0-0	178,464	240,240	247,104	157,872	157,872	981,552
11-1-1-0	2028	12,168	24,336	44,616	75,036	158,184
11-2-0-0	936	5616	11,232	20,592	34,632	73,008
12-1-0-0	0	0	0	0	2028	2028
13-0-0-0	0	0	0	0	4	4
All 39	624,368,943,360	8,972,493,400	1,441,035,444	203,578,240	27,509,156	635,013,559,600

Study 8J37 Main

Top Hits and Misses

Unique Ranks

The late Margie Gwozdzinsky of New York City was a first-rate player with an eccentric personality, which I guess might be expected from the way she spelled her last name. Too many Z’s there, girl! Margie’s penchant for the extraordinary was to look for hands that had 13 unique card ranks. For example, A-Q-J-8-6 5-3-2 K-9-7 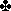10-4 would bring immediate joy, having one card of each rank.

Toward the other extreme, a bridge hand may contain as few as four different ranks, e.g., A-Q-9-8 A-Q-9 A-Q-8 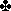Q-9-8. The great majority of hands fall in between in a high-biased bell curve, with nine different ranks being the most common.

The following table shows the percent chance of each number of different ranks for each generic hand pattern. Percents are relative to the generic pattern in that row, except Total percents (last column) are relative to all bridge hands. The bottom row shows the percents for all generic patterns combined. Percents shown as 0.0000 are not zero but round that way to the nearest 10,000th.

Percents for Different Ranks

Pattern	4	5	6	7	8	9	10	11	12	13	Total
4-4-3-2	0.0002	0.0269	0.7954	7.2155	25.1870	37.0885	23.3196	5.8694	0.4898	0.0079	21.5512
5-3-3-2	0	0.0157	0.6270	6.4623	24.2543	37.4506	24.3570	6.2889	0.5354	0.0088	15.5168
5-4-3-1	0	0.0094	0.4665	5.5034	22.7192	37.6968	25.9527	7.0201	0.6214	0.0105	12.9307
5-4-2-2	0	0.0115	0.5287	5.9121	23.4296	37.6321	25.2254	6.6716	0.5793	0.0097	10.5797
4-3-3-3	0.0003	0.0360	0.9332	7.8317	25.9501	36.7923	22.4707	5.5261	0.4524	0.0072	10.5361
6-3-2-2	0	0	0.2586	4.3991	21.1614	38.1314	27.6134	7.7240	0.7000	0.0121	5.6425
6-4-2-1	0	0	0.1862	3.6641	19.5225	37.9878	29.2258	8.5882	0.8110	0.0145	4.7021
6-3-3-1	0	0	0.2257	4.0650	20.4165	38.0661	28.3463	8.1168	0.7505	0.0132	3.4482
5-5-2-1	0	0.0038	0.3004	4.4134	20.8248	37.8692	27.8923	7.9493	0.7338	0.0129	3.1739
4-4-4-1	0.0001	0.0164	0.5980	6.1882	23.7063	37.4535	24.8995	6.5598	0.5688	0.0095	2.9932
7-3-2-1	0	0	0	1.7741	15.3081	37.6184	33.3720	10.8102	1.0965	0.0207	1.8808
6-4-3-0	0	0	0.1467	3.1664	18.1769	37.6375	30.5345	9.3965	0.9243	0.0171	1.3262
5-4-4-0	0	0.0049	0.3130	4.3816	20.5389	37.6683	28.1520	8.1608	0.7668	0.0137	1.2433
5-5-3-0	0	0.0027	0.2391	3.8415	19.4891	37.6547	29.2109	8.7100	0.8368	0.0152	0.8952
6-5-1-1	0	0	0.0993	2.6165	16.8191	37.4133	31.8616	10.1474	1.0234	0.0193	0.7053
6-5-2-0	0	0	0.0897	2.4476	16.2333	37.1317	32.4248	10.5642	1.0878	0.0209	0.6511
7-2-2-2	0	0	0	1.9515	16.0459	37.9716	32.6708	10.3171	1.0241	0.0190	0.5130
7-4-1-1	0	0	0	1.4193	13.7295	36.7567	34.8740	11.9295	1.2662	0.0248	0.3918
7-4-2-0	0	0	0	1.3179	13.1791	36.3367	35.3954	12.3991	1.3448	0.0269	0.3617
7-3-3-0	0	0	0	1.4976	14.0178	36.8417	34.5983	11.7732	1.2470	0.0245	0.2652
8-2-2-1	0	0	0	0	7.9300	34.0869	40.3834	15.7412	1.8207	0.0379	0.1924
8-3-1-1	0	0	0	0	7.4151	33.3099	40.8822	16.4067	1.9448	0.0414	0.1176
7-5-1-0	0	0	0	0.8786	10.7943	34.5168	37.6547	14.4343	1.6855	0.0359	0.1085
8-3-2-0	0	0	0	0	7.0289	32.6340	41.2408	16.9894	2.0620	0.0448	0.1085
6-6-1-0	0	0	0.0269	1.3493	12.4260	35.3012	36.0857	13.2733	1.5062	0.0314	0.0723
8-4-1-0	0	0	0	0	6.0247	30.8768	42.1732	18.5046	2.3669	0.0538	0.0452
9-2-1-1	0	0	0	0	0	22.1211	48.0655	25.9900	3.7324	0.0910	0.0178
9-3-1-0	0	0	0	0	0	20.3335	47.7676	27.5955	4.1958	0.1076	0.0100
9-2-2-0	0	0	0	0	0	21.3018	47.9290	26.7258	3.9448	0.0986	0.0082
7-6-0-0	0	0	0	0.4079	7.3427	30.5944	40.7925	18.3566	2.4476	0.0583	0.0056
8-5-0-0	0	0	0	0	4.3512	27.1950	43.5120	21.7560	3.1080	0.0777	0.0031
10-2-1-0	0	0	0	0	0	0	44.3787	45.8580	9.4675	0.2959	0.0011
9-4-0-0	0	0	0	0	0	17.6224	46.9930	30.2098	5.0350	0.1399	0.0010
10-1-1-1	0	0	0	0	0	0	45.5166	45.1980	9.0123	0.2731	0.0004
10-3-0-0	0	0	0	0	0	0	41.9580	47.2028	10.4895	0.3497	0.0002
11-1-1-0	0	0	0	0	0	0	0	71.5976	27.2189	1.1834	0.0000
11-2-0-0	0	0	0	0	0	0	0	70.5128	28.2051	1.2821	0.0000
12-1-0-0	0	0	0	0	0	0	0	0	92.3077	7.6923	0.0000
13-0-0-0	0	0	0	0	0	0	0	0	0	100	0.0000
All 39	0.0001	0.0151	0.5511	5.8309	22.9885	37.4231	25.6202	6.9423	0.6182	0.0106	100

Exact Hand Counts for Different Ranks

Pattern	4	5	6	7	8	9	10	11	12	13	Total
4-4-3-2	205,920	36,756,720	1,088,493,120	9,874,584,720	34,469,154,720	50,756,706,000	31,913,481,600	8,032,424,400	670,269,600	10,810,800	136,852,887,600
5-3-3-2	0	15,444,000	617,760,000	6,367,561,200	23,898,786,912	36,901,584,720	23,999,976,000	6,196,750,560	527,567,040	8,648,640	98,534,079,072
5-4-3-1	0	7,722,000	383,011,200	4,518,914,400	18,655,116,480	30,953,482,560	21,310,248,960	5,764,318,560	510,269,760	8,648,640	82,111,732,560
5-4-2-2	0	7,722,000	355,212,000	3,971,887,920	15,740,524,800	25,282,136,880	16,947,010,080	4,482,157,680	389,188,800	6,486,480	67,182,326,640
4-3-3-3	183,040	24,092,640	624,349,440	5,239,874,640	17,362,144,800	24,616,191,600	15,034,219,200	3,697,293,600	302,702,400	4,804,800	66,905,856,160
6-3-2-2	0	0	92,664,000	1,576,214,640	7,582,262,688	13,662,689,040	9,894,044,160	2,767,564,800	250,810,560	4,324,320	35,830,574,208
6-4-2-1	0	0	55,598,400	1,094,052,960	5,829,183,360	11,342,691,360	8,726,477,760	2,564,321,760	242,161,920	4,324,320	29,858,811,840
6-3-3-1	0	0	49,420,800	890,089,200	4,470,482,016	8,335,126,800	6,206,840,640	1,777,295,520	164,324,160	2,882,880	21,896,462,016
5-5-2-1	0	772,200	60,540,480	889,512,624	4,197,184,992	7,632,424,800	5,621,616,000	1,602,160,560	147,891,744	2,594,592	20,154,697,992
4-4-4-1	11,440	3,114,540	113,667,840	1,176,215,040	4,505,941,440	7,118,911,800	4,732,728,000	1,246,845,600	108,108,000	1,801,800	19,007,345,500
7-3-2-1	0	0	0	211,891,680	1,828,322,496	4,492,968,480	3,985,787,520	1,291,118,400	130,965,120	2,471,040	11,943,524,736
6-4-3-0	0	0	12,355,200	266,666,400	1,530,809,280	3,169,726,560	2,571,528,960	791,350,560	77,837,760	1,441,440	8,421,716,160
5-4-4-0	0	386,100	24,710,400	345,945,600	1,621,620,000	2,974,051,080	2,222,700,480	644,323,680	60,540,480	1,081,080	7,895,358,900
5-5-3-0	0	154,440	13,590,720	218,378,160	1,107,890,784	2,140,538,400	1,660,538,880	495,134,640	47,567,520	864,864	5,684,658,408
6-5-1-1	0	0	4,447,872	117,189,072	753,296,544	1,675,674,000	1,427,025,600	454,486,032	45,837,792	864,864	4,478,821,776
6-5-2-0	0	0	3,706,560	101,189,088	671,134,464	1,535,133,600	1,340,539,200	436,756,320	44,972,928	864,864	4,134,297,024
7-2-2-2	0	0	0	63,567,504	522,666,144	1,236,858,480	1,064,194,560	336,061,440	33,359,040	617,760	3,257,324,928
7-4-1-1	0	0	0	35,315,280	341,621,280	914,593,680	867,746,880	296,833,680	31,505,760	617,760	2,488,234,320
7-4-2-0	0	0	0	30,270,240	302,702,400	834,593,760	812,972,160	284,787,360	30,888,000	617,760	2,296,831,680
7-3-3-0	0	0	0	25,225,200	236,107,872	620,539,920	582,753,600	198,300,960	21,003,840	411,840	1,684,343,232
8-2-2-1	0	0	0	0	96,864,768	416,370,240	493,281,360	192,277,800	22,239,360	463,320	1,221,496,848
8-3-1-1	0	0	0	0	55,351,296	248,648,400	305,173,440	122,470,920	14,517,360	308,880	746,470,296
7-5-1-0	0	0	0	6,054,048	74,378,304	237,837,600	259,459,200	99,459,360	11,613,888	247,104	689,049,504
8-3-2-0	0	0	0	0	48,432,384	224,864,640	284,169,600	117,065,520	14,208,480	308,880	689,049,504
6-6-1-0	0	0	123,552	6,198,192	57,081,024	162,162,000	165,765,600	60,972,912	6,918,912	144,144	459,366,336
8-4-1-0	0	0	0	0	17,297,280	88,648,560	121,080,960	53,127,360	6,795,360	154,440	287,103,960
9-2-1-1	0	0	0	0	0	25,019,280	54,362,880	29,395,080	4,221,360	102,960	113,101,560
9-3-1-0	0	0	0	0	0	12,972,960	30,476,160	17,606,160	2,676,960	68,640	63,800,880
9-2-2-0	0	0	0	0	0	11,119,680	25,019,280	13,951,080	2,059,200	51,480	52,200,720
7-6-0-0	0	0	0	144,144	2,594,592	10,810,800	14,414,400	6,486,480	864,864	20,592	35,335,872
8-5-0-0	0	0	0	0	864,864	5,405,400	8,648,640	4,324,320	617,760	15,444	19,876,428
10-2-1-0	0	0	0	0	0	0	3,088,800	3,191,760	658,944	20,592	6,960,096
9-4-0-0	0	0	0	0	0	1,081,080	2,882,880	1,853,280	308,880	8580	6,134,700
10-1-1-1	0	0	0	0	0	0	1,144,000	1,135,992	226,512	6864	2,513,368
10-3-0-0	0	0	0	0	0	0	411,840	463,320	102,960	3432	981,552
11-1-1-0	0	0	0	0	0	0	0	113,256	43,056	1872	158,184
11-2-0-0	0	0	0	0	0	0	0	51,480	20,592	936	73,008
12-1-0-0	0	0	0	0	0	0	0	0	1872	156	2028
13-0-0-0	0	0	0	0	0	0	0	0	0	4	4
All 39	400,400	96,164,640	3,499,651,584	37,026,941,952	145,979,817,984	237,641,564,160	162,691,809,280	44,084,232,192	3,925,868,544	67,108,864	635,013,559,600

Margie meets Magnus?

Another interesting pursuit is a hand that meets both Margie’s 13 unique card ranks and Magnus’s lowest-card length identifier in each suit. A little thought reveals there can be only three hand types:

Hand Type	Choose x	Combinations	Ways	Hands
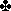x-x-x-x-x-6 x-x-5-4 3-2 A	K Q J 10 9 8 7	21	24	504
K-Q-J-10-9-8-7 x-x-3 x-2 A	6 5 4	3	24	72
x-x-x-x-x-x-7 x-6-5-4 3-2 —	A K Q J 10 9 8	7	24	168

Combinations shows the number of distinct ‘x’ choices. Ways shows the number of suit permutations. Totaling the last column shows there are only 744 such hands. Hank Aaron hit more home runs than that (755 if I recall). Considering there are 635+ billion bridge hands, don’t hold your breath for one of these.

Study 8J37 Main

Top Hits and Misses

Alphabetic Suits

David Burn of London, England, renowned UK expert and journalist, asked what is remarkable about this hand: A-J-7-6 8-5-4 K-3-2 Q-10-3. Well, it looks pretty ordinary aside from almost being a “Margie” — achieved simply by changing either of the threes to a nine. In fact it’s an oddity of a different sort. The card ranks in each suit are alphabetic, i.e., ace-jack-seven-six, eight-five-four, king-three-two and queen-ten-three are each in correct order. Note that holdings such as A-J-5-4 or Q-9-3 would not be acceptable.

Of the 8192 possible suit holdings, only 376 qualify as alphabetic. The longest alphabetic suit is seven cards, of which only three possibilities exist: A-K-Q-7-6-3-2, A-K-9-7-6-3-2 and A-J-9-7-6-3-2. Obviously any singleton must qualify, and so will a void suit to be consistent with other oddities. Now there’s a job for you: Alphabetize a void. My kind of work!

The following table shows the percent chance of each number of alphabetic suits for each generic hand pattern. Hit percents are relative to the generic pattern in that row. Total percents (last column) are relative to all bridge hands. The bottom row shows the percents for all generic patterns combined. Percents shown as 0.0000 are not zero but round that way to the nearest 10,000th.

Percents for Alphabetic Suits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	14.5069	44.4331	32.5785	7.8753	0.6063	21.5512
5-3-3-2	12.2937	40.7982	36.0377	10.3957	0.4747	15.5168
5-4-3-1	0	50.8325	41.3243	7.5422	0.3010	12.9307
5-4-2-2	8.2059	36.7750	45.3690	9.2680	0.3821	10.5797
4-3-3-3	21.7334	41.2939	28.2099	8.0095	0.7532	10.5361
6-3-2-2	6.4535	31.1341	45.0435	17.1537	0.2152	5.6425
6-4-2-1	0	26.6841	61.8731	11.3063	0.1365	4.7021
6-3-3-1	0	39.9767	46.2068	13.6470	0.1695	3.4482
5-5-2-1	0	28.7538	64.1661	6.8904	0.1897	3.1739
4-4-4-1	0	59.9838	33.4238	6.2081	0.3844	2.9932
7-3-2-1	0	20.3606	54.8348	24.7614	0.0432	1.8808
6-4-3-0	0	52.9801	40.8028	6.1441	0.0730	1.3262
5-4-4-0	0	67.3671	28.7832	3.7201	0.1296	1.2433
5-5-3-0	0	57.0894	38.9918	3.8172	0.1015	0.8952
6-5-1-1	0	0	93.5021	6.4302	0.0677	0.7053
6-5-2-0	0	29.9686	65.5944	4.3909	0.0460	0.6511
7-2-2-2	3.2868	20.9099	44.3535	31.3949	0.0548	0.5130
7-4-1-1	0	0	84.1882	15.7844	0.0274	0.3918
7-4-2-0	0	26.9834	62.2639	10.7341	0.0186	0.3617
7-3-3-0	0	40.4251	46.2709	13.2809	0.0231	0.2652
8-2-2-1	0	10.2728	43.5569	46.1703	0	0.1924
8-3-1-1	0	0	63.6364	36.3636	0	0.1176
7-5-1-0	0	0	94.5508	5.4400	0.0092	0.1085
8-3-2-0	0	20.3963	54.8951	24.7086	0	0.1085
6-6-1-0	0	0	97.4523	2.5312	0.0164	0.0723
8-4-1-0	0	0	84.3357	15.6643	0	0.0452
9-2-1-1	0	0	32.0513	67.9487	0	0.0178
9-3-1-0	0	0	63.6364	36.3636	0	0.0100
9-2-2-0	0	10.2728	43.5569	46.1703	0	0.0082
7-6-0-0	0	0	98.5454	1.4524	0.0022	0.0056
8-5-0-0	0	0	94.7164	5.2836	0	0.0031
10-2-1-0	0	0	32.0513	67.9487	0	0.0011
9-4-0-0	0	0	84.3357	15.6643	0	0.0010
10-1-1-1	0	0	0	100	0	0.0004
10-3-0-0	0	0	63.6364	36.3636	0	0.0002
11-1-1-0	0	0	0	100	0	0.0000
11-2-0-0	0	0	32.0513	67.9487	0	0.0000
12-1-0-0	0	0	0	100	0	0.0000
13-0-0-0	0	0	0	100	0	0.0000
All 39	8.5730	40.8031	40.5359	9.6775	0.4106	100

Exact Hand Counts for Alphabetic Suits

Pattern	No Hit	1 Hit	2 Hits	3 Hits	4 Hits	Total
4-4-3-2	19,853,051,400	60,808,000,968	44,584,556,640	10,777,568,256	829,710,336	136,852,887,600
5-3-3-2	12,113,446,800	40,200,176,016	35,509,371,456	10,243,314,432	467,770,368	98,534,079,072
5-4-3-1	0	41,739,476,688	33,932,106,624	6,193,025,280	247,123,968	82,111,732,560
5-4-2-2	5,512,927,500	24,706,302,600	30,479,938,956	6,226,437,456	256,720,128	67,182,326,640
4-3-3-3	14,540,906,016	27,628,065,920	18,874,093,056	5,358,852,096	503,939,072	66,905,856,160
6-3-2-2	2,312,310,000	11,155,544,400	16,139,330,064	6,146,265,840	77,123,904	35,830,574,208
6-4-2-1	0	7,967,559,600	18,474,579,552	3,375,927,984	40,744,704	29,858,811,840
6-3-3-1	0	8,753,480,736	10,117,659,552	2,988,201,216	37,120,512	21,896,462,016
5-5-2-1	0	5,795,247,900	12,932,483,148	1,388,735,712	38,231,232	20,154,697,992
4-4-4-1	0	11,401,323,804	6,352,976,448	1,179,988,992	73,056,256	19,007,345,500
7-3-2-1	0	2,431,774,800	6,549,206,976	2,957,383,728	5,159,232	11,943,524,736
6-4-3-0	0	4,461,833,376	3,436,296,864	517,435,776	6,150,144	8,421,716,160
5-4-4-0	0	5,318,872,452	2,272,538,160	293,712,384	10,235,904	7,895,358,900
5-5-3-0	0	3,245,338,824	2,216,551,584	216,997,248	5,770,752	5,684,658,408
6-5-1-1	0	0	4,187,791,608	287,996,280	3,033,888	4,478,821,776
6-5-2-0	0	1,238,991,600	2,711,868,192	181,534,320	1,902,912	4,134,297,024
7-2-2-2	107,062,500	681,105,000	1,444,737,600	1,022,633,304	1,786,524	3,257,324,928
7-4-1-1	0	0	2,094,800,292	392,752,620	681,408	2,488,234,320
7-4-2-0	0	619,763,400	1,430,097,408	246,543,480	427,392	2,296,831,680
7-3-3-0	0	680,896,944	779,360,400	223,696,512	389,376	1,684,343,232
8-2-2-1	0	125,482,500	532,045,800	563,968,548	0	1,221,496,848
8-3-1-1	0	0	475,026,552	271,443,744	0	746,470,296
7-5-1-0	0	0	651,501,864	37,483,992	63,648	689,049,504
8-3-2-0	0	140,540,400	378,254,448	170,254,656	0	689,049,504
6-6-1-0	0	0	447,663,216	11,627,616	75,504	459,366,336
8-4-1-0	0	0	242,131,032	44,972,928	0	287,103,960
9-2-1-1	0	0	36,250,500	76,851,060	0	113,101,560
9-3-1-0	0	0	40,600,560	23,200,320	0	63,800,880
9-2-2-0	0	5,362,500	22,737,000	24,101,220	0	52,200,720
7-6-0-0	0	0	34,821,864	513,216	792	35,335,872
8-5-0-0	0	0	18,826,236	1,050,192	0	19,876,428
10-2-1-0	0	0	2,230,800	4,729,296	0	6,960,096
9-4-0-0	0	0	5,173,740	960,960	0	6,134,700
10-1-1-1	0	0	0	2,513,368	0	2,513,368
10-3-0-0	0	0	624,624	356,928	0	981,552
11-1-1-0	0	0	0	158,184	0	158,184
11-2-0-0	0	0	23,400	49,608	0	73,008
12-1-0-0	0	0	0	2028	0	2028
13-0-0-0	0	0	0	4	0	4
All 39	54,439,704,216	259,105,140,428	257,408,256,216	61,453,240,784	2,607,217,956	635,013,559,600

Alphabetic Magnus hit?

Only 45 of 8192 possible suit holdings qualify as alphabetic Magnus hits. Besides a void and singleton ace, these include every doubleton with the two, and alphabetized tripletons with the lowest card three. Curiously, only one holding of 4+ cards qualifies, specifically A-8-5-4, so that must appear at least once in any complete hand that qualifies. For example, A-8-5-4 9-6-3 J-7-3 K-10-3.

Margie knows the ABC’s

Hands that qualify as a “Margie” (13 unique ranks) with each suit alphabetic are more common than one might think, 58,368 by my count, but still rare in the grand scheme of 635+ billion bridge hands. For example, 8-5-4-3 A-K-10 Q-7-2 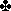J-9-6, or A-J-9-7-6-3-2 K-Q-10 8-5-4 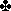--, the latter having the longest possible suit.

Alphabetic and symmetric?

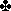Only 10 of 8192 possible suit holdings are both alphabetic and symmetric: Void, singleton 8, A-2, K-3, 9-7, A-8-2, A-K-3-2, A-9-7-2, K-9-7-3 and A-K-9-7-3-2. These can produce 412 hands (counting all combinations and suit permutations), e.g., A-K-9-7-3-2 A-8-2 K-3 9-7.

Crack! There’s a deep line drive into the left-center gap. This will be extra bases!
He’s rounding second… rounding third… Here comes the relay… Oh no!
Thrown out at the plate! (Just like this study should have been.)

Study 8J37 Main

Top Hits and Misses

© 2019 Richard Pavlicek